Introducción
Hoy voy a comenzar una serie llamada «Algoritmos que todo programador debe conocer». En esta serie, analizaremos varios algoritmos como búsqueda, clasificación, gráficos, matriz, etc.
Hoy comenzando con la primera parte de la serie con el algoritmo de búsqueda. Vamos a ver 4 algoritmos de búsqueda que todo programador debería conocer. ¡Comencemos!
Búsqueda lineal
En informática, una búsqueda lineal o secuencial es un método para encontrar un elemento dentro de una lista. Comprueba secuencialmente cada elemento de la lista hasta que se encuentra una coincidencia o se ha buscado en toda la lista.
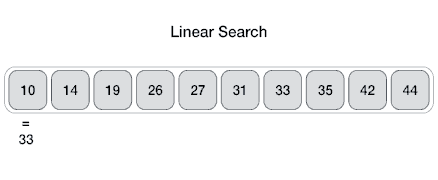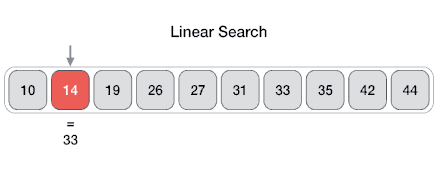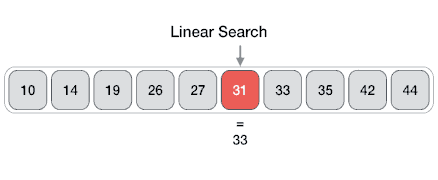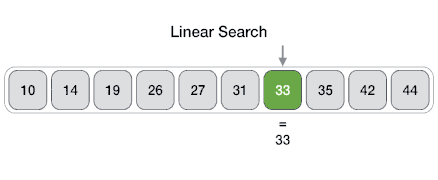
En la búsqueda lineal, buscamos el elemento de destino en la lista en orden secuencial uno por uno desde el primer elemento de la lista hasta el último.
Mejor caso: el valor a encontrar está en la primera posición de la lista
Peor de caso: el valor a encontrar es la última posición de la lista
Cuándo se debe usar:
- Cuando la lista no está ordenada
- Cuando la lista es pequeña
Búsqueda binaria
En informática, la búsqueda binaria, también conocida como búsqueda de medio intervalo, búsqueda logarítmica o corte binario, es un algoritmo de búsqueda que encuentra la posición de un valor objetivo dentro de una matriz ordenada. La búsqueda binaria compara el valor objetivo con el elemento intermedio de la matriz. Si no son iguales, se elimina la mitad en la que el objetivo no puede estar y la búsqueda continúa en la mitad restante, tomando nuevamente el elemento del medio para compararlo con el valor objetivo.

En la búsqueda binaria, la lista debe estar ordenada. Buscamos el valor objetivo eligiendo el valor del medio de la lista y comparándolo. Si no coincide, si el valor objetivo es menor que el elemento del medio, la mitad inicial se eliminará; de lo contrario, se eliminará la mitad final. El proceso continuará hasta que encontremos el valor objetivo.
Mejor caso: el valor objetivo está en la posición media de la lista
Peor de caso: el valor objetivo se encuentra en la primera o última posición de la lista
Cuándo usar:
- Cuando la lista está ordenada
- Cuando la lista es grande
Búsqueda en profundidad (DFS)
La búsqueda en profundidad (Depth First Search) es un algoritmo para recorrer o buscar estructuras de datos de árbol o gráfico. El algoritmo comienza en el nodo raíz (seleccionando algún nodo arbitrario como nodo raíz en el caso de un gráfico) y explora en la medida de lo posible a lo largo de cada rama antes de retroceder.

En DFS, elegimos la raíz del gráfico, árbol o estructura de datos y exploramos cada rama en orden. Cuando se selecciona una rama, explora todas sus sub-ramas antes de cambiar a una rama diferente.
Mejor caso: el valor objetivo está en la posición de la raíz del árbol
Peor de caso: el valor objetivo está en la punta de una sub-rama de la última rama ordenada
Cuándo usar:
Cuando el árbol es muy ancho
Cuando el valor objetivo se encuentra en la profundidad del árbol.
Búsqueda de amplitud (BFS)
La búsqueda en amplitud (Breadth First Search) es un algoritmo para recorrer o buscar estructuras de datos de árbol o gráfico. Comienza en la raíz del árbol (o algún nodo arbitrario de un gráfico, a veces denominado «clave de búsqueda»), y explora todos los nodos vecinos en la profundidad actual antes de pasar a los nodos del siguiente nivel de profundidad.
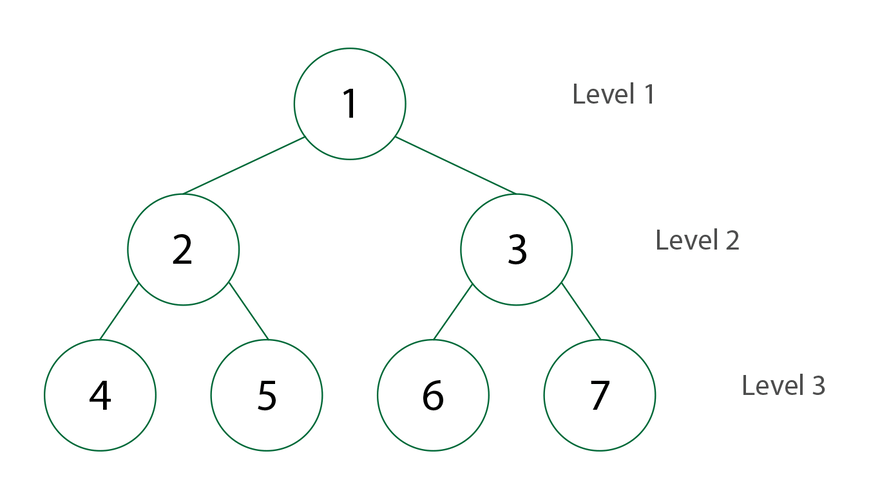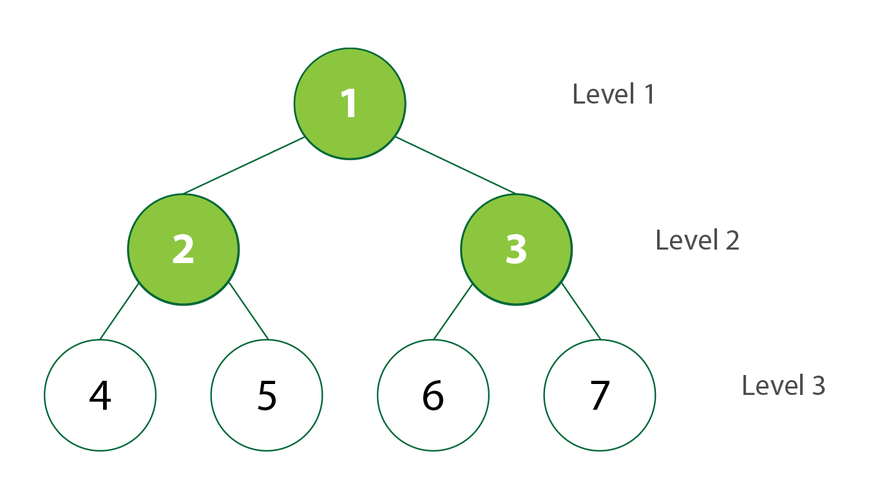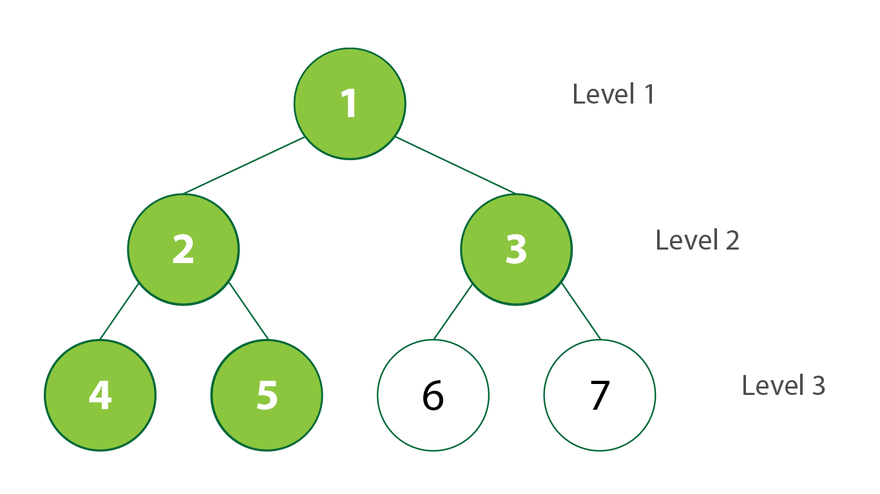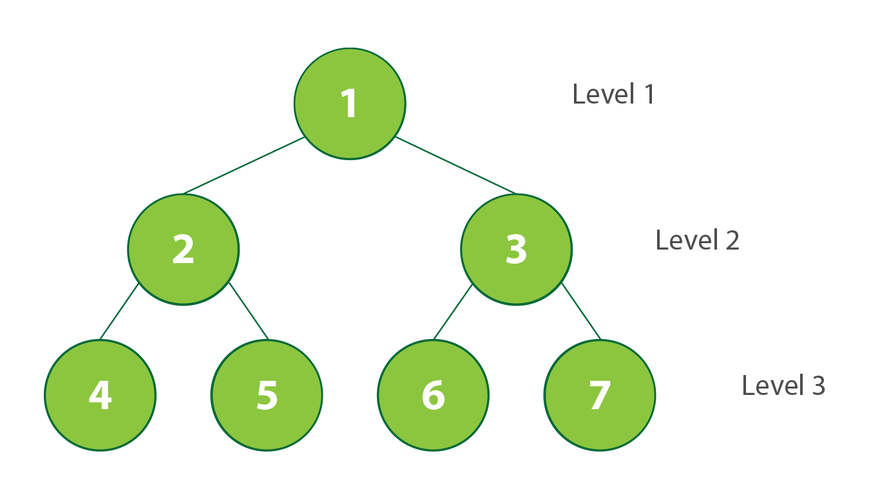
En BSF, al igual que en DFS, elegimos el nodo raíz del gráfico, árbol o estructura de datos. Después del nodo, nos movemos a todos sus nodos adyacentes y luego al siguiente nivel que es todo el nodo adyacente a la rama.
Mejor caso: el valor objetivo está en la posición de la raíz del árbol
Peor caso: el valor objetivo se encuentra en la punta de la rama más larga del árbol
Cuándo usar:
- Cuando el valor objetivo no está lejos de la raíz del árbol
- Cuando el árbol es muy profundo y el valor objetivo es raro.
Puedes leer el artículo original en inglés en: https://dev.to/surajondev/algorithms-every-programmer-should-know-part-1-searching-algorithm-1hd3